Calculate tonality indicators

This example shows how to calculate tonality indicators. The list of indicators covered in this example is:

• Annex C of ISO1996-2

• DIN45681

• ECMA418-2

• ISO/TS 20065

• Aures

All these indicators are calculated using the same acoustic signal, and the results are commented, compared, and discussed.

Set up analysis

Setting up the analysis consists of loading Ansys libraries, connecting to the DPF server, and retrieving the example file.

# Load required libraries.
from ansys.sound.core.examples_helpers import download_aircraft10kHz_wav
from ansys.sound.core.psychoacoustics import (
    TonalityAures,
    TonalityDIN45681,
    TonalityECMA418_2,
    TonalityISO1996_2,
    TonalityISO1996_2_OverTime,
    TonalityISOTS20065,
)
from ansys.sound.core.server_helpers import connect_to_or_start_server
from ansys.sound.core.signal_utilities import LoadWav
from ansys.sound.core.spectrogram_processing.stft import Stft

# Connect to a remote server or start a local server.
my_server = connect_to_or_start_server(use_license_context=True)

# Load example data from a WAV file: flyover noise of an aircraft.
path_aircraft_wav = download_aircraft10kHz_wav(server=my_server)
wav_loader = LoadWav(path_aircraft_wav)
wav_loader.process()
signal_aircraft = wav_loader.get_output()[0]

The signal used in this example is the flyover noise of an aircraft. The signal is sampled at 10 kHz, and the duration is about 26 seconds.

# Calculate and display the spectrogram of the signal used in this example.
stft = Stft(signal_aircraft, fft_size=1024, window_overlap=0.8)
stft.process()
stft.plot()

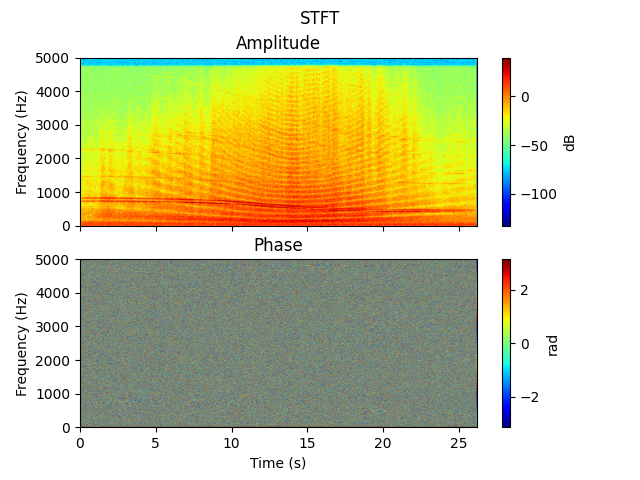
From the spectrogram, you can see that the signal contains some tonal components, especially the two tones whose frequencies start at around 800 Hz and decrease over the duration of the signal, due to the Doppler effect.

ISO 1996-2 annex C

In this section, we calculate and print out the tonal audibility of the signal according to annex C of the standard ISO 1996-2 using the class TonalityISO1996_2.

# Calculate the ISO 1996-2 tonality.
tonality_ISO1996_2 = TonalityISO1996_2(signal=signal_aircraft)
tonality_ISO1996_2.process()

# Display the results in the console.
print(
    f"ISO 1996-2 tonality: \n"
    f"- tonal audibility: {tonality_ISO1996_2.get_tonal_audibility():.1f} dB\n"
    f"- tonal adjustment: {tonality_ISO1996_2.get_tonal_adjustment():.1f} dB"
)

ISO 1996-2 tonality:
- tonal audibility: 0.0 dB
- tonal adjustment: 0.0 dB

You can also retrieve computation details using the method get_computation_details(). As you can notice, computing the ISO 1996-2 tonality over the whole signal is not relevant, as the tonal audibility equals 0 dB in that case, even if strong tonal components are audible. Rigorously speaking, the ISO 1996-2 standard requires at least 1 minute of stationary signal, which is often a very high bar to reach, especially for transient signals. The ISO 1996-2 tonality is therefore not very useful for the analysis of transient signals, and it is recommended to use the ISO 1996-2 tonality over time in that case.

Let us now calculate and plot the ISO 1996-2 tonality over time using the class TonalityISO1996_2_OverTime.

# Calculate the ISO 1996-2 tonality over time.
tonality_ISO1996_2_over_time = TonalityISO1996_2_OverTime(signal=signal_aircraft)
tonality_ISO1996_2_over_time.process()

# Display the results over time in a figure.
tonality_ISO1996_2_over_time.plot()

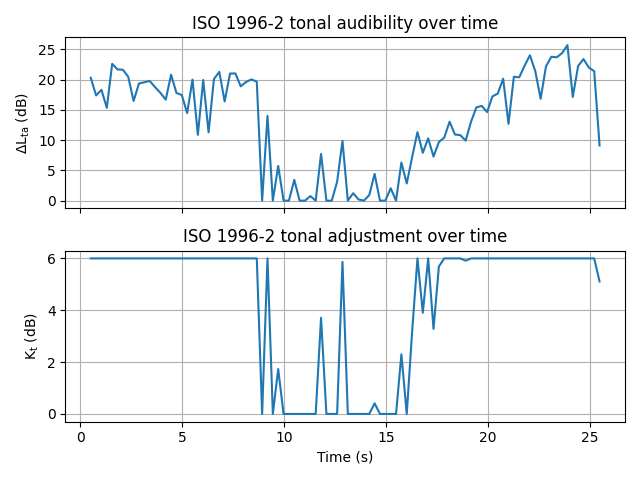
In this figure, you can notice that the tonal audibility and tonal adjustment show strong tonal components near the beginning and the end of the signal. Some tonal content is also detected in the middle part of the signal, but less consistently so. The most likely reason is that, due to the Doppler effect, the frequencies of the tones are changing at a higher rate than in the other parts of the signal.

DIN 45681

In this section, we calculate, print out, and plot the tonality according to the DIN 45681 standard using the same signal and the class TonalityDIN45681.

# Calculate the DIN 45681 tonality.
tonality_DIN45681 = TonalityDIN45681(signal=signal_aircraft)
tonality_DIN45681.process()

# Display the overall results in the console.
print(
    f"DIN 45681 tonality: \n"
    f"- mean difference: {tonality_DIN45681.get_mean_difference():.1f} dB "
    f"(+/-{tonality_DIN45681.get_uncertainty():.1f} dB)\n"
    f"- tonal adjustment: {tonality_DIN45681.get_tonal_adjustment():.1f} dB"
)

DIN 45681 tonality:
- mean difference: 15.1 dB (+/-1.1 dB)
- tonal adjustment: 6.0 dB

The DIN 45681 tonality returns results in a similar form as the ISO 1996-2 tonality. However, as it is an average of the computed tonality over time, the overall DIN 45681 tonality value is more relevant than that of ISO 1996-2, which computes tonality over the entire signal at once.

# Display the results over time in a figure.
tonality_DIN45681.plot()

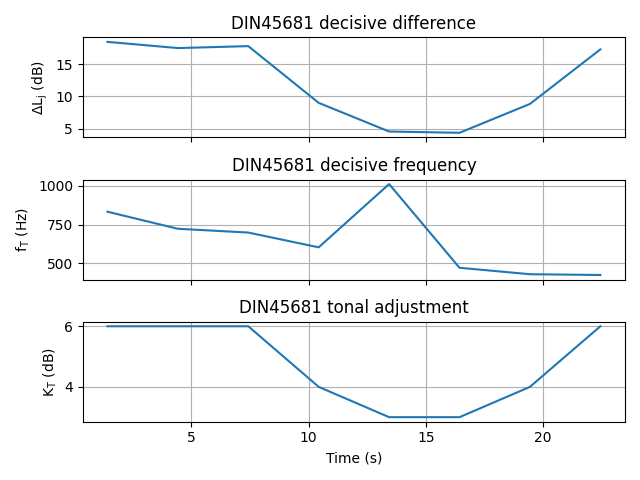
The DIN 45681 “decisive difference”, displayed in the figure, is comparable in its definition to the ISO 1996-2 tonal audibility over time. However the default time resolution for the computation of the two indicators is different (3 s for DIN 45681, 250 ms for ISO 1996-2). In both cases, you can change this time resolution using the class properties TonalityDIN45681.window_length for DIN 45681, and TonalityISO1996_2_OverTime.window_length and TonalityISO1996_2_OverTime.overlap for ISO 1996-2. Additionally, the DIN 45681 class provides the frequency of the most prominent tone at each computation time step, with the method TonalityDIN45681.get_decisive_frequency_over_time().

ISO/TS 20065

In this section, we calculate, print out, and plot the tonality according to the ISO/TS 20065 standard using the same signal and the class TonalityISOTS20065.

# Calculate the ISO/TS 20065 tonality.
tonality_ISOTS20065 = TonalityISOTS20065(signal=signal_aircraft)
tonality_ISOTS20065.process()

# Display the overall results in the console.
print(
    f"ISO/TS 20065 tonality (mean audibility): {tonality_ISOTS20065.get_mean_audibility():.1f} dB "
    f"(+/- {tonality_ISOTS20065.get_uncertainty():.1f} dB)"
)

# Display the results over time in a figure.
tonality_ISOTS20065.plot()

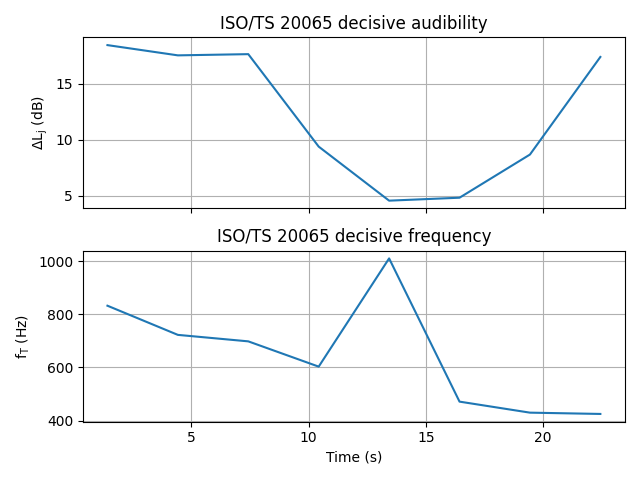
ISO/TS 20065 tonality (mean audibility): 15.2 dB (+/- 1.1 dB)

As you can see from the results, the ISO/TS 20065 tonality is basically the same as the DIN 45681 tonality. Nonetheless a few minor differences are noteworthy:

• the DIN 45681 standard computes a tonal adjustment Kt, meant to be used as a dBA penalty when the sound has tonal components, whereas the ISO/TS 20065 standard does not.

• the DIN 45681 standard can detect tones down to 90 Hz, whereas this limit is extended to 50 Hz in the ISO/TS 20065 standard. This means that a very low frequency tone (that is, between 50 and 90 Hz) can be detected by the ISO/TS 20065 standard, but will most likely be missed by the DIN 45681 standard.

• Some minor differences in the calculation of the detected tones’ edge slopes.

Aures

In this section, we calculate, print out, and plot the tonality according to Aures model using the same signal and the class TonalityAures.

# Calculate the Aures tonality.
tonality_Aures = TonalityAures(signal=signal_aircraft)
tonality_Aures.process()

# Display the overall results in the console.
print(f"Aures tonality: {tonality_Aures.get_tonality():.1f} tu")

Aures tonality: 0.2 tu

Contrary to previously mentioned tonality standards, Aures tonality is meant to model the perceptual scale of tonality, which is known to have a non-linear relation to spectral peak emergence as expressed in decibels. It uses a specific unit called tonality unit (tu), using as a reference a 1-kHz pure tone with a level of 60 dB SPL, which is assigned a tonality of 1 tu.

# Display the results over time in a figure.
tonality_Aures.plot()

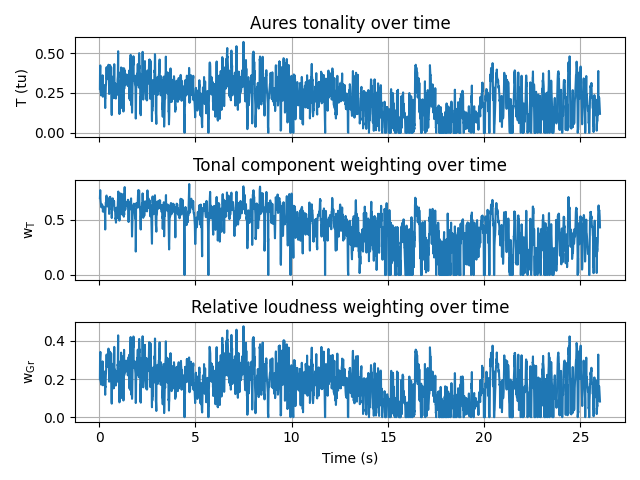
The figure plots the the Aures tonality over time, which is the main value of interest, and the tonal component weighting and relative loudness weighting, which are two intermediate multiplicative parameters used to calculate the tonality.

ECMA 418-2

In this section, we calculate, print out, and plot the tonality according to the ECMA 418-2 standard using the same signal and the class TonalityECMA418_2.

# Calculate the ECMA 418-2 tonality.
tonality_ECMA418_2 = TonalityECMA418_2(signal=signal_aircraft)
tonality_ECMA418_2.process()

# Display the overall results in the console.
print(
    "Tonality ECMA 418-2 (psychoacoustic tonality): "
    f"{tonality_ECMA418_2.get_tonality():.1f} tuHMS"
)

Tonality ECMA 418-2 (psychoacoustic tonality): 1.3 tuHMS

As with the Aures tonality, the ECMA 418-2 standard uses a perceptual scale, with a specific unit called tuHMS (tonality unit, hearing model of Sottek). The hearing model of Sottek is a perceptual model of sound, where the tonality is computed based on autocorrelation functions calculated in each critical band. A value of 1 tuHMS corresponds to the tonality of a 1-kHz pure tone with a level of 40 dB SPL. A value of 0 tuHMS indicates that no tonality could be detected (that is, no tonal content), while high values in tuHMS indicate prominent tonal contents.

# Display the results over time in a figure.
tonality_ECMA418_2.plot()

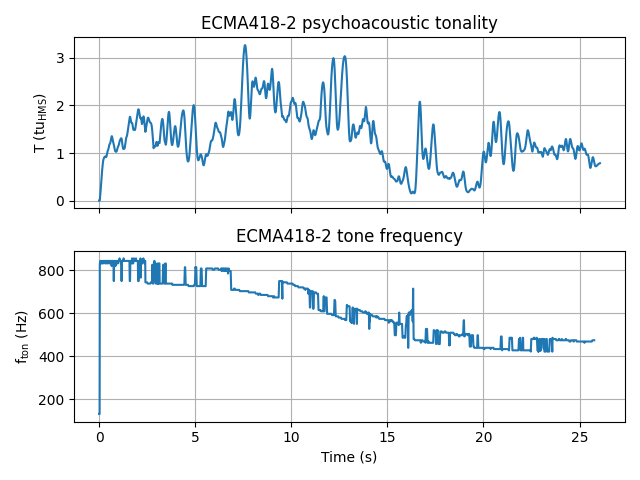
The figure shows the psychoacoustic tonality over time, as well as the frequency of the most prominent tone at each computation time step. The frequency seemingly follows the Doppler effect that the previously displayed spectrogram showed, only switching back and forth between the two main tones’ frequencies.